01 점화식 Recurrence formula
수열의 항 사이에 성립하는 관계식
점화식은 자기 호출을 사용하는 함수(재귀함수, recursive function)의 복잡도를 구하는데 유용함
factorial (n) {
if(n=1) return 1;
return n*factorial(n-1) }
Divide-and-conquer (분할 정복)
1. 주어진 문제를 작은 단위 (subproblem) 로 쪼갠다. 이 때 subproblem 은 본문제와 같지만 input size (입력 값) 가 작은 문제를 뜻한다. → Divide
2. 1번에서 나눈 subproblem 들을 (recursively 하게) 해결한다. → Conquer
3. 2번에서 푼 subproblem 들의 답을 적절하게 조합 (combine, merge) 해서 본 문제의 답을 제시. → Conquer
Merge sort (only concept)
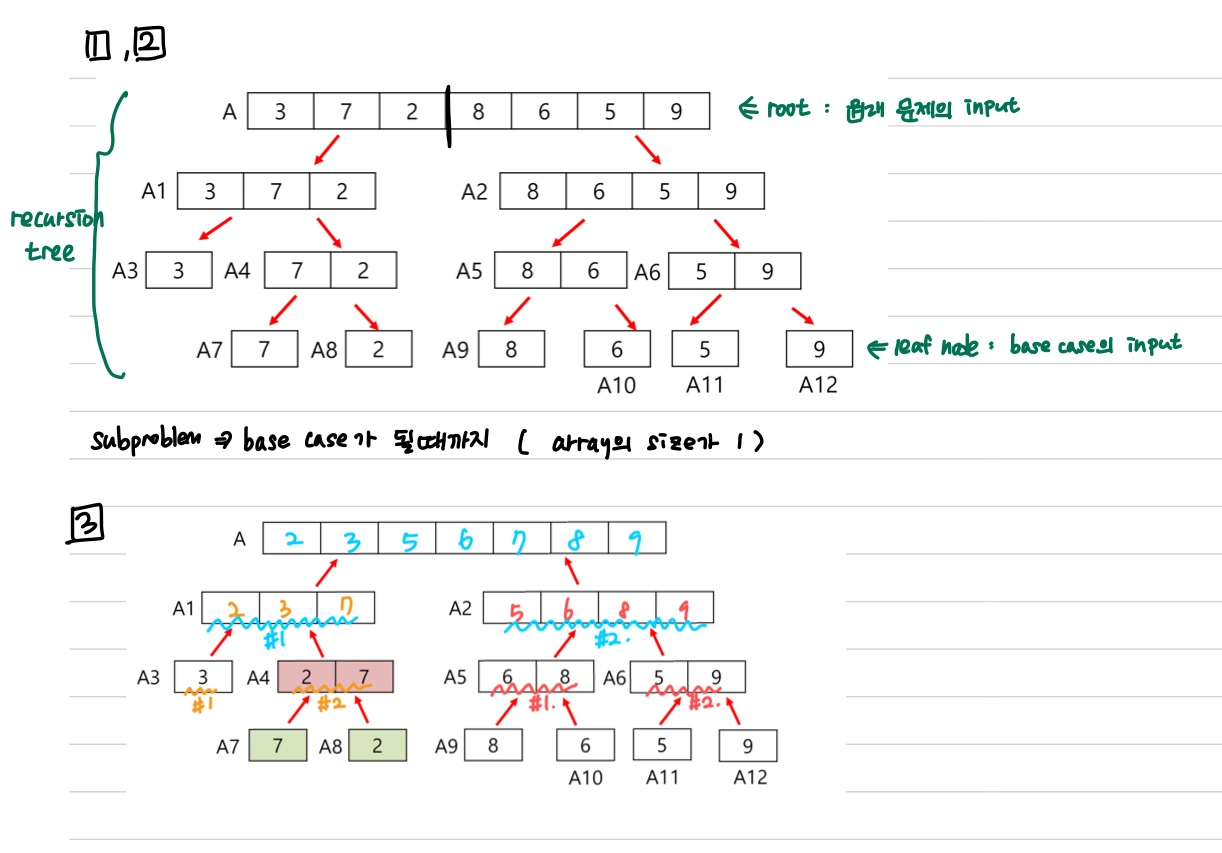
02 점화식의 점근적 분석 방법
1. 반복 대치
반복적으로 치환해서 점근적 복잡도를 구하는 방법 (= 더 작은 문제에 대한 함수로 반복해서 대치해 나가는 해법)
Ex1 팩토리얼 문제
T(n) = T(n-1) + c
Ex2 병합 정렬
2. 추정 후 증명
- 결론을 추정하고 수학적 귀납법을 이용해 증명하는 방법
- 식의 모양을 보고 점근적 복잡도를 추정하고, 이를 수학적 귀납적으로 증명하는 방법
- 수학적 귀납법의 다양한 가정과 전개
① n = k일 때 성립하면, n = k+1 일 때도 성립
② n 0 ≤ k < n인 모든 k에 대해 성립하면, n일 때도 성립
③ n = k 일 때 성립하면, n = 2k일 때도 성립
Ex3 병합 정렬
T(n) = 2T( 𝑛/ 2 )+ n의 점근적 복잡도는 T(n)=O(nlogn)이다.
즉 충분히 큰 n에 대해서 T(n) ≤ cnlogn인 양의 상수 c가 존재한다.

3. 마스터 정리
'전공 > 알고리즘' 카테고리의 다른 글
| 중간고사 (0) | 2022.10.27 |
|---|---|
| Ch05. 선택 알고리즘 (0) | 2022.10.27 |
| Ch01, Ch02 (0) | 2022.10.26 |
| Ch06 검색트리 (0) | 2022.10.26 |
| HW#1 (0) | 2022.10.18 |